Exame de Física II

Cursos de Química e Eng. Química -23/1/99

I ( 5 valores )

Considere 3 planos infinitos carregados uniformemente e perpendiculares ao eixo dos zz, conforme indicado na figura. O espaço entre os planos 1 e 2 está preenchido por um dieléctrico linear, homogéneo e isótropo de constante dieléctrica $\epsilon$.

a) Determine $\vec E$, $\vec D$ e $\vec P$ em todo o espaço.

b) Faça um gráfico de D_z em função de z. Relacione as descontinuidades de D_z com as densidades de carga nos planos carregados.

c) Calcule $V=\phi_1-\phi_2$.

d) Determine as densidades de carga de polarização à superfície do dieléctrico, $\sigma'$.

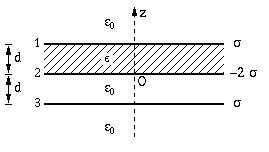
Fig. 1

II ( 4 valores )

Seja um circuito OAC com a forma dum sector circular de abertura ${\pi \over 2}$. Tem-se |OA| = |OC| = r. A resistência eléctrica do circuito é R. O circuito, sempre assente no plano Oxy, roda em torno de O com velocidade angular $\omega$. Existe um campo $\vec B$ uniforme paralelo ao eixo dos zz, e tendo intensidades diferentes nos diferentes quadrantes conforme indicado na figura.

a) Mostre que existe corrente induzida. Justifique a resposta com base na lei da indução de Faraday ou com base na lei de Laplace.
Nota: Nesta alínea só precisa de explicar porque é que existe corrente, não é preciso fazer as contas.

b) Calcule o fluxo do campo de indução magnética $\vec B$ através do circuito. Trace o gráfico da função i = i(t) para $0<\omega t<\pi$, supondo que no instante t=0 a espira se encontra na posição indicada na figura.

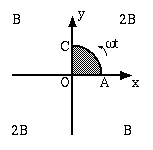
Fig. 2

III ( 5 valores )

Uma onda plana electromagnética propaga-se num meio não condutor e não magnético ($\sigma=0$, $\mu_r=1$, $\rho=0$ e $\vec J =0$). O campo $\vec E$ é dado por:

$$\left\{ \begin{array} {ll} E_x &= 0 \cr \vbox to 20 pt{} E_y... ...{\sqrt{5}}\, y + \alpha \, z \right) \right]\end{array}\right.$$

Sabe-se que a frequência é $f=1\ MHz$, o índice de refracção do meio é n=1.5 e $E_0=10^{-2}\ V/m$.

a) Determine $\alpha$ de forma a que as expressões correspondam de facto a uma onda plana electromagnética.

b) Qual a direcção de propagação da onda?

c) Qual a polarização da onda?

d) Escreva as componentes do campo magnético $\vec H$.

IV ( 6 valores )

Considere um electrãopotencial de Coulomb do átomo de hidrogénio. O electrão-se no estado

$$\psi_1(\vec r,0)=A\ \hbox{\raise .5ex\hbox{$\chi $}}_{211}(\vec r)\ .$$

a) Qual o valor da constante A (real e positiva)? Escreva a expressão$\psi_1(\vec r,t)$.

b) Qual o valor médio de E, L² e L_z para o estado $\psi_1$?

c) Para o estado $\psi_1$ determine a posição do máximo da distribuiçãoprobabilidade radial P(r).

d) Qual o valor médio de r no estado $\psi_1(\vec r,t)$?

e) Considere agora que o electrãoinstante t=0 se encontra no estado

$$\psi_2(\vec r,0)= {1 \over \sqrt{3}}\ \hbox{\raise .5ex\hbox... ... + B\ \hbox{\raise .5ex\hbox{$\chi $}}_{3 \ell 1} (\vec r) \ .$$

Sabendo que $\left\langle L^2\right\rangle=2 \hbar^2$ determine o valor de $\ell$ em $\hbox{\raise .5ex\hbox{$\chi $}}_{3\ell 1}$.

f) Qual a probabilidade duma medida de L_z no estado $\psi_2$ dar o valor próprio $-\hbar$?

Formulário e Constantes

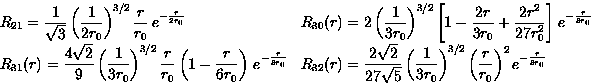
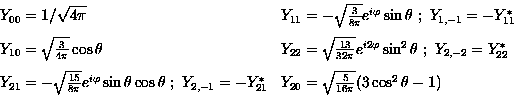
$$\begin{array} {ll}\displaystyle R_{21}={1 \over \sqrt{3}} \l... ... \left({r \over r_0}\right)^2 e^{- {r \over 3 r_0}} \end{array}$$

$$\begin{array} {ll} Y_{00}=1/\sqrt{4\pi}& Y_{11} = - \sqrt{{3... ...20} = \sqrt{{5 \over 16 \pi}} (3 \cos^2 \theta - 1)\end{array}$$

$$E_n=-E_0 {1 \over n^2}\ ; \ E_0=13.6\ eV \ ; \ \int_0^{\infty}x^n e^{-x}\ dx = n!$$

$$c=3 \times 10^8\ \hbox{m/s} \ ; \ \varepsilon_0=8.85 \times ... ...ox{H/m}\ ; \ Z_0=\sqrt{\mu_0 \over \varepsilon_0}=376.8 \Omega$$