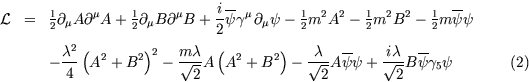
onde o fermião
Considere o modelo de Wess e Zumino descrito pelo Lagrangiano seguinte
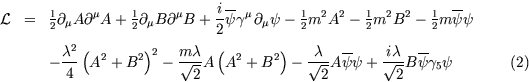
onde o fermião ![]() é uma partícula de Majorana e A e B
são campos escalares reais.
é uma partícula de Majorana e A e B
são campos escalares reais.
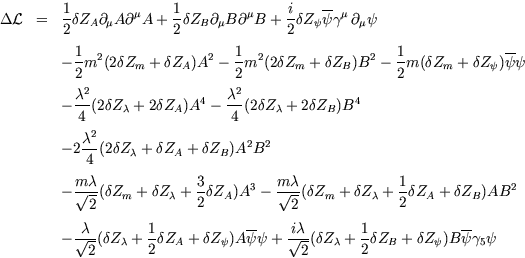
Mostre que as 6 constantes de renormalização estão todas relacionadas, só há uma independente, uma renormalização da função de onda. Para isso calcule todas as constantes em MS (subtração mínima).
Nota. Para este trabalho é conveniente consultar a nova versão do Apêndice do livro de Introdução à Teoria do Campo que pode ser obtida por ftp no seguinte endereço: ftp://porthos.ist.utl.pt/pub/textos/tc1apendice.ps.gz.