Métodos Funcionais em QED:Funcionais Geradores

O funcional gerador das funções de Green para QED é dado por

$$Z(J_{\mu},\eta,\overline{\eta})= \int {\cal D}(A_{\mu},\psi,... ...}+J^{\mu}A_{\mu} +\overline{\eta}\psi+\overline{\psi}\eta)} \ .$$

onde

$$\begin{eqnarray} &&{\cal L}_{QED}=-{1 \over 4}\ F_{\mu \nu} F^{\mu \nu} + \overl... ...)^2 \nonumber\\ && D_{\mu}=\partial_{\mu}+i e A_{\mu} \ .\nonumber\end{eqnarray}$$

1.

Calcule $Z_0[J^{\mu},\eta,\overline{\eta}]$

2.

Mostre que

$$Z[J^{\mu},\eta,\overline{\eta}]=\exp \left\{ (-e) \int d^4x ... ...\mu}(x)} \right\}Z_0[J^{\mu},\eta,\overline{\eta}] \ .\nonumber$$

3.

Expanda

$$Z=Z_0 \left[ 1+ (-ie) Z_1+(-ie)^2 Z_2 + \cdots \right] \nonumber$$

onde se retiraram as amplitudes vácuo-vácuo em Z_i, isto é, $Z_i[0]=0 \rightarrow Z[0]=1$. Mostre que

4.

Discuta os factores numéricos e os sinais das expressões anteriores.

5.

Calcule em ordem mais baixa

$$\left\langle 0\right\vert T A^{\mu}(x) \psi_{\beta}(y) \over... ...ha}(z) i \delta \overline{\eta}_{\beta}(y) i \delta J_{\mu}(x)}$$

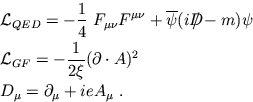
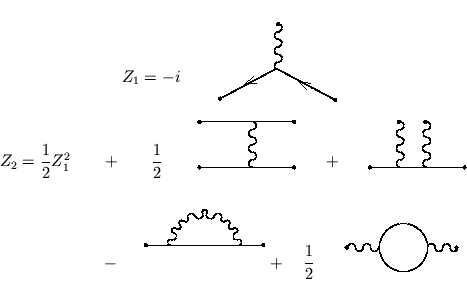
e verifique que coincide com as regras de Feynman para o vértice.

6.

Calcule a amplitude para o efeito de Compton em ordem mais baixa, isto é

$$\left\langle 0\right\vert T A^{\mu}(x) A^{\nu} (y) \psi_{\be... ...overline{\eta}_{\beta}(z) i \delta J_{\nu}(y) i \delta J_{\mu}}$$

e verifique que reproduz o que se obtém usando as regras de Feynman usuais.