Next: Soluções Estáticas em Teorias Não Abelianas Up: No Title Previous: Métodos Funcionais em QED:Funcionais Geradores
![]()
![]()
![]()
Next: Soluções Estáticas em Teorias Não Abelianas
Up: No Title
Previous: Métodos Funcionais em QED:Funcionais Geradores
As identidades de Ward para QED deduzidas na secção 1.7 não têm a forma
![]()
onde ![]() pois
pois
![]()
não é invariante para transformações de gauge. Introduza o funcional
![]()
onde
![]()
e
![]()
onde ![]() e
e ![]() são campos escalares anticomutativos.
são campos escalares anticomutativos.
![]()
onde ![]() não depende das fontes nem dos campos. Explique porque
é que esta renormalização (infinita) não afecta o
cálculo das funções
de Green. Assim tanto Z como Z' servem para o cálculo destas.
não depende das fontes nem dos campos. Explique porque
é que esta renormalização (infinita) não afecta o
cálculo das funções
de Green. Assim tanto Z como Z' servem para o cálculo destas.
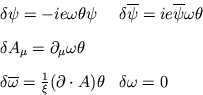
onde ![]() é um parâmetro anticomutativo constante (variável
de Grassman).
é um parâmetro anticomutativo constante (variável
de Grassman).
![]()
Mostre que
![]()
onde
![]()
Considere os funcionais ![]() , WG e W e ainda
, WG e W e ainda ![]() ,
,![]() e
e ![]() definidos de maneira semelhante. Qual a relação
entre
definidos de maneira semelhante. Qual a relação
entre ![]() , WG e W e entre
, WG e W e entre ![]() ,
,![]() e
e ![]() .
.
![]()
![]()
Escreva as identidades de Ward para
![]() . Mostre que
conduzem aos resultados conhecidos
. Mostre que
conduzem aos resultados conhecidos