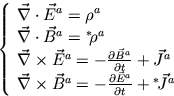

Next: Renormalização da Electrodinâmica Escalar
Up: No Title
Previous: Ansatze de Wu-Yang
- 1.
- Mostre que o tensor
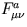 dos campos de
Yang-Mills
satisfaz as identidades de Bianchi:
dos campos de
Yang-Mills
satisfaz as identidades de Bianchi:
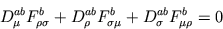
ou
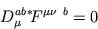
onde
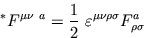
- 2.
- Explique o significado geométrico da Identidades de
Bianchi.
Sugestão: Veja o artigo de R.P. Feynman em Les Houches,
Session XXIX, 1976, North Holland, 1977, Pags: 135-140.
- 3.
- Considere a teoria de Yang-Mills (YM) sem matéria.
- (a)
- Mostre que as eqs. de YM sem matéria se podem escrever na
forma
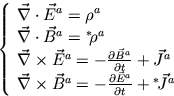
calcule 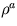 ,
, 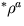 ,
, 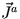 e
e 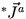 .
. - (b)
- Mostre que as 4-correntes
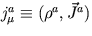 e
e
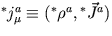 são conservadas.
são conservadas.
- 4.
- Mostre que
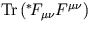 é uma 4-divergência. Comente sobre a sua inclusão na acção.
é uma 4-divergência. Comente sobre a sua inclusão na acção.
6/17/1999
![]()
![]()
![]()
![]()
![]()
![]()