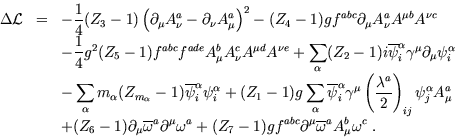Next: Renormalização da Cromodinâmica Quântica (QCD) Up: Home Page TFP Previous: QED numa gauge não linear
![]()
![]()
![]()
Next: Renormalização da Cromodinâmica Quântica (QCD)
Up: Home Page TFP
Previous: QED numa gauge não linear
Considere a teoria que descreve as interacções dos quarks com os gluões (QCD) descrita pelo Lagrangeano
![]()
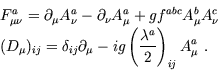
O índice ![]() referencia os diferentes
sabores de quarks (up,down,...,top).
Para quantificar a teoria considere a condição de gauge
referencia os diferentes
sabores de quarks (up,down,...,top).
Para quantificar a teoria considere a condição de gauge
![]()
para a qual resulta o Lagrangeano dos fantasmas
![]()
Para renormalizar a teoria necessitamos do seguinte Lagrangeano de contratermos: